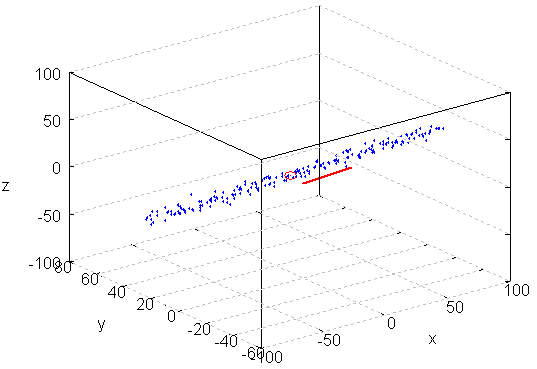
Gerade in drei Dimensionen
Regressionsgerade in einen Datensatz mit drei Dimensionen mittels der Methode der kleinsten Quadrate ermitteln.
1. Lösungsanssatz
Beschreibung der Geraden mit zwei getrennten Gleichungsystemen unter der Bedingung, dass die Gerade nicht parallel zur x-y-Ebene ist.
x = mx*z + cx
y = my*z + cy
2. Die passende Geradengleichung
Parameterdarstellung (p, r und p0 sind Vektoren)
g: p = lambda*r + p0
Ortsvektor eines Punktes auf der Geraden
p0 = [cx;cy;0]
Richtungsvektor
r = [mx;my;1]
3. Octave-Code
clear
clc
% ============================================
% Abschnitt 1: Datensatz erzeugen und anzeigen
% ============================================
% Eine Gerade sei gegeben durch
p0c = [4 10 2];
rc = [6 -5 6];
u=-10:.1:10;
% Datensatz mit einer normal verteilten Streuung aufbauen
g = u.'*rc + ones(length(u),1)*p0c;
gn = randn(size(g))*3 + g;
x=gn(:,1);
y=gn(:,2);
z=gn(:,3);
% Punktwolke darstellen
hold off
h=plot3(x,y,z,'o');
set(h, 'markersize',.6);
xlabel('x');
ylabel('y');
zlabel('z');
hold on
% ========================================
% Abschnitt 2: Regressionsgerade ermitteln
% ========================================
% Hier nehmen wir an p0c und r0c wären unbekannt
% Lösung von zwei getrennten Gleichungsystemen
% x = mx*z + cx
% y = my*z + cy
p = polyfit(z,x,1);
mx = p(1);
cx = p(2);
p = polyfit(z,y,1);
my = p(1);
cy = p(2);
% Ein Punkt auf der Geraden ist p0
p0 = [cx;cy;0]
h=plot3(p0(1),p0(2),p0(3),'ro');
set(h, 'markersize',4);
l=20;
% Richtungsvektor r
r = [mx;my;1]
h = plot3([0 mx]*l,[0 my]*l,[0 1]*l,'r.-');
set(h, 'markersize',4);
set(h, 'linewidth',2);
% Die Steigung der Geraden mit zunehmenden z
m = sqrt(mx^2 + my^2)
grid on
clc
% ============================================
% Abschnitt 1: Datensatz erzeugen und anzeigen
% ============================================
% Eine Gerade sei gegeben durch
p0c = [4 10 2];
rc = [6 -5 6];
u=-10:.1:10;
% Datensatz mit einer normal verteilten Streuung aufbauen
g = u.'*rc + ones(length(u),1)*p0c;
gn = randn(size(g))*3 + g;
x=gn(:,1);
y=gn(:,2);
z=gn(:,3);
% Punktwolke darstellen
hold off
h=plot3(x,y,z,'o');
set(h, 'markersize',.6);
xlabel('x');
ylabel('y');
zlabel('z');
hold on
% ========================================
% Abschnitt 2: Regressionsgerade ermitteln
% ========================================
% Hier nehmen wir an p0c und r0c wären unbekannt
% Lösung von zwei getrennten Gleichungsystemen
% x = mx*z + cx
% y = my*z + cy
p = polyfit(z,x,1);
mx = p(1);
cx = p(2);
p = polyfit(z,y,1);
my = p(1);
cy = p(2);
% Ein Punkt auf der Geraden ist p0
p0 = [cx;cy;0]
h=plot3(p0(1),p0(2),p0(3),'ro');
set(h, 'markersize',4);
l=20;
% Richtungsvektor r
r = [mx;my;1]
h = plot3([0 mx]*l,[0 my]*l,[0 1]*l,'r.-');
set(h, 'markersize',4);
set(h, 'linewidth',2);
% Die Steigung der Geraden mit zunehmenden z
m = sqrt(mx^2 + my^2)
grid on