Ortskurve


Als Ortskurve wird in der Systemtheorie die graphische Darstellung einer von einem reellen Parameter abhängigen komplexen Systemgröße bezeichnet. Die komplexe Systemgröße kann z.B. ein Übertragungsverhalten eines Filters sein oder der Widerstand eines LCR-Netzwerks sein. In der Elektrotechnik ist der reelle Parameter meist die Frequenz einer Sinusschwingung.

Eine oder mehrere Ortskurven werden in der Elektrotechnik entweder

Elektrotechnik für Ingenieure 2
Wilfried Weißgerber
http://books.google.de/books/about/Elektrotechnik_f%C3%BCr_Ingenieure_2.html?hl=de&id=atXN-iHst7MC

Ortskurve für einen RC-Tiefpass


Es soll die Ortskurve der Spannungsübertragungsfunktion eines RC-Tiefpasses berechnet werden.

Die Übertragungsfunktion lautet

{{lf code="H(\omega) = \frac{U_{out}(\omega)}{U_{in}(\omega)}"}}

Die beiden Spannungen am Eingang und am Ausgang können als Produkt aus Strom und Widerstand geschrieben werden, wobei der Widerstand des Kondensator eine Frequenzabhängigkeit besitzt.

{{lf code="U_{out}(\omega) = i \cdot \frac{1 }{j\omega C }"}}

{{lf code="U_{in}(\omega) = i \cdot \left( \frac{1 }{j\omega C } + R \right)"}}

Yes
Code: \omega = 2\pi f
Latex formula: \omega = 2\pi f


Ortskurve für einen belasteten RC-Tiefpass mit C = 100 nF, R1 = 10 kOhm


Das passende Octave-Skript zum Plot von oben
clear;clc
R = 10E3;
C = 100E-9;

f =logspace(0,4,40); % Frequenz von 1 Hz bis 10 kHz

w = 2*pi*f; % Kreisfrequenz

% Übertragungsgleichung
Zout = 1 ./ (1i*w*C);
Zin = Zout + R;
H = Zout ./ Zin;

% Plot
plot(H,'.-');
ylabel('Im (H)')
xlabel('Re (H)')
for k=1:length(w)
    fk = round(f(k));
    text(real(H(k)),imag(H(k)), [ num2str(fk) ' Hz' ])
end
grid
axis("equal")




Ortskurve für einen belasteten RC-Tiefpass


Es soll die Ortskurve der Spannungsübertragungsfunktion eines RC-Tiefpasses (R1, C) mit ohmscher Belastung (R2) berechnet werden.

Die Übertragungsfunktion lautet allgemein

{{lf code="H(\omega) = \frac{U_{out}(\omega)}{U_{in}(\omega)}"}}

Die beiden Spannungen am Eingang und am Ausgang können als Produkt aus Strom und Widerstand geschrieben werden, wobei der Widerstand des Kondensator eine Frequenzabhängigkeit besitzt.

{{lf code="U_{out}(\omega) = i \cdot Z_1(\omega)"}}

{{lf code="U_{in}(\omega) = i \cdot Z_2(\omega)"}}

wobei Z1 und Z2 komplexe Widerstände sind

Z1 ist die Parallelschaltung aus C und R2
{{lf code="Z_1(\omega) = \frac{1 }{ \frac{1}{R_2} + j\omega C }"}}

Z2 ist die Serienschaltung aus R1 und Z1 (Gesamtimpedanz)
Yes
Code: Z_2(\omega) = Z_1(\omega) + R_1
Latex formula: Z_2(\omega) = Z_1(\omega) + R_1


Die Übertragungsfunktion lässt sich als Quotient der Impedanzen Z1 und U2 ausdrücken
{{lf code="H(\omega) = \frac{Z_1(\omega)}{Z_2(\omega)}"}}



Ortskurve für einen belasteten RC-Tiefpass mit C = 100 nF, R1 = 10 kOhm und der Last R2 = 100 k



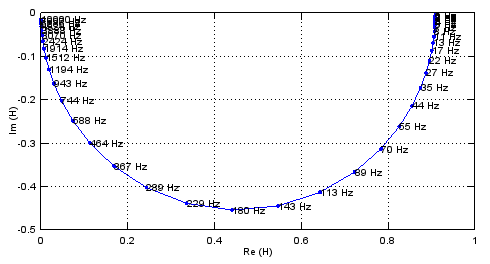
Das passende Octave-Skript zum Plot von oben
clear;clc
R1 = 10E3;
C = 100E-9;
R2 = 100E3;

f =logspace(0,4,40); % Frequenz von 1 Hz bis 10 kHz

w = 2*pi*f; % Kreisfrequenz

% Übertragungsgleichung
Z1 = 1 ./ ( (1./ R2) + (1i*w*C) );
Z2 = Z1 + R1;
H = Z1 ./ Z2;

% Plot
plot(H,'.-');
ylabel('Im (H)')
xlabel('Re (H)')
for k=1:length(w)
    fk = round(f(k));
    text(real(H(k)),imag(H(k)), [ num2str(fk) ' Hz' ])
end
grid
axis("equal")



Ortskurve für ein doppeltes LCR-Filter


Ein Filter bestehend aus 2 Spulen jeweils 6 uH mit einem Serienwiderstand von jeweils 30 mOhm, zwei Widerständen, zwei Elkos, einmal 2200 uF bis 50 V und 470 uF bis 100 V bilden ein zweistufiges LCR-Glied. Die Bauelemente sind so gewählt, weil es eine der wenigen Elkos waren, die eine höhere Spannung als 48 V aufweisen und diese in der Schublade meines Heimlabors lagen. Das gleiche gilt für die Spulen. Die Elkos sollten mindestens 48 V vertragen, da diese Schaltung für die Filterung der Phantomspannung eines Mischpultes verwendet wird (PhantomspannungMM122 Projektseite). Funktioniert mit diesem Filter wunderbar!



Die Übertragungsfunktion lautet

{{lf code="H(\omega) = \frac{U_{out}(\omega)}{U_{in}(\omega)} =\frac{Z_{C2} }{ Z_{L2}+R_2+Z_{C2} \left[ \left(\frac{1}{Z_{C1} } + \frac{1}{Z_{L2}+R_2+Z_{C2} } \right) \left(Z_{L1} + R_1 \right) + 1 \right] }"}}

wobei

{{lf code="Z_{C1} = \frac{1}{j\omega C_1}"}}

{{lf code="Z_{C2} = \frac{1}{j\omega C_2}"}}

{{lf code="Z_{L1} = j\omega L_1"}}

{{lf code="Z_{L2} = j\omega L_2"}}

Yes
Code: \omega = 2\pi f
Latex formula: \omega = 2\pi f


Ortskurve der Übertragungsfunktion, berechnet mit Octave


Frequenzgang der Übertragungsfunktion, berechnet mit Octave


Das Octave-Skript dazu
clear;clc
L  = 6E-6;
RL = 30E-3; % Serienwiderstand der Spule (gemessen 30 mV an 1 A Gleichstrom)
C1 = 2.2E-3;
C2 = 470E-6;
R1 = 1/3*10; % Drei Widerstände 10 Ohm parallel jeweils 1/4 Watt
R2 = R1;
f =logspace(-1,2.4,40); % Frequenz von 1 Hz bis 10 kHz

w = 2*pi*f; % Kreisfrequenz

% Komplexe Widerstände
s = 1i*w;
ZC1 = 1 ./ (s*C1);  
ZC2 = 1 ./ (s*C2);
ZL1  = s*L + RL;
ZL2  = ZL1;


% Übertragungsgleichung Herleitung
i1i2 = (1 ./ ZC1) .* ( ZL2 + R2 + ZC2 );
H2 = ZC2 ./ ( (i1i2 .* (ZL1 + R1)) + (2 * (ZL2 + R2)) + ZC2  );

% Übertragungsgleichung Kontrollherleitung
Z2 = ZL2 + R2 + ZC2;
H = ZC2 ./ ( Z2 .* ( ( (1 ./ ZC1) + (1 ./ Z2) ) .* (ZL1 + R1) + 1 ) );

% Ortskurve plotten
figure(1)
hold off
plot(H,'.-');
hold on
plot(H2,'.-r');

ylabel('Im (H)')
xlabel('Re (H)')
for k=1:length(w)
    fk = round(f(k)*10)/10;
    text(real(H(k)),imag(H(k)), [ num2str(fk) ' Hz' ])
end
axis("equal")
grid

% Übertragungsfunktion linear
figure(2)
plot(f,abs(H),'.-')
ylabel('|H(f)|')
xlabel('f (Hz)')
grid

% Übertragungsfunktion logarithmisch
figure(3)
plot(f,20*log(abs(H)),'.-')
ylabel('|H(f)|')
xlabel('f (Hz)')


Frequenzgang der Übertragungsfunktion aus einer Simulation mit Spice zur Kontrolle






Siehe auch • • • •
Valid XHTML :: Valid CSS: :: Powered by WikkaWiki